صيغ النزوح الزاوي وتمارين حلها

ال النزوح الزاوي يتم إنشاؤه عندما يتحرك كائن باتباع مسار أو مسار له شكل دائرة. إنه يختلف عن النزوح ؛ بينما يقيس الإزاحة الزاوية الزاوية المقطوعة ، يقيس الإزاحة المسافة.

لحساب الإزاحة الزاوية لكائن يتحرك على طول محيط ، يمكن استخدام طريقتين: إذا كانت الزاوية الأولية والنهائية معروفة ، فسيكون الإزاحة الزاوية هي الطرح بين الزاوية النهائية والزاوية الأولية.

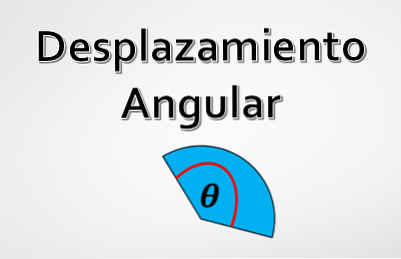
إذا كان طول الإزاحة (طول القوس المحيطي سافر) ونصف قطر المحيط معروفين ، فإن الإزاحة الزاوية تعطى بواسطة θ = l / r.

مؤشر

• 1 الصيغ
• 2 تمارين
  • 2.1 التمرين الأول
  • 2.2 التمرين الثاني
  • 2.3 التمرين الثالث
• 3 المراجع

الصيغ

للحصول على الصيغ الموضحة أعلاه ، يمكنك مشاهدة الصور التالية:

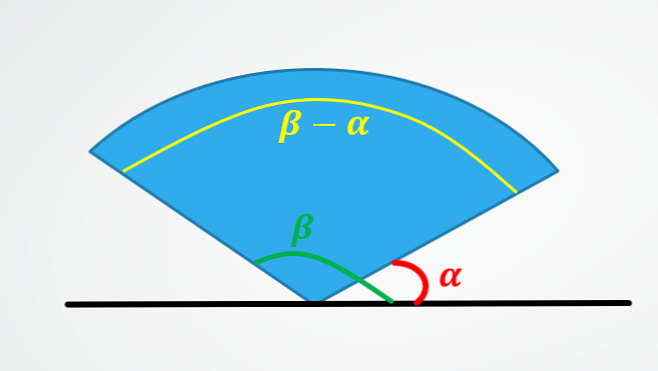
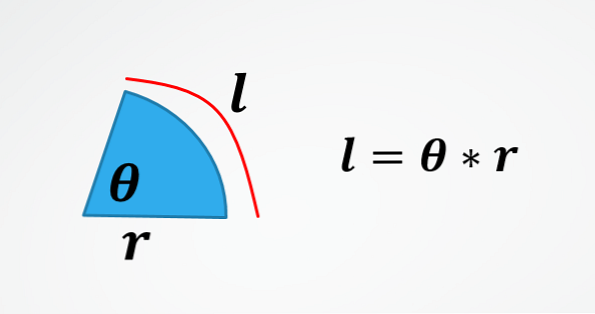
أول واحد يوضح لماذا يساوي الإزاحة الزاوية الطرح من الزاوية النهائية ناقص الزاوية الأولية.

في الصورة الثانية هي صيغة لطول قوس الدائرة. لذلك ، عن طريق مسح - تحصل على الصيغة الموصوفة في البداية.

تدريب

فيما يلي بعض التمارين التي يجب أن يطبق فيها تعريف الإزاحة الزاوية وحيث يتم استخدام الصيغ الموصوفة أعلاه.

التمرين الأول

ركض خوان مسافة 35 مترًا على حلبة سباق دائرية يبلغ قطر نصفها 7 أمتار. حساب النزوح الزاوي الذي قدم خوان.

حل

نظرًا لأن مسافة القوس المقطوعة ونصف قطر المحيط معروف ، يمكن تطبيق الصيغة الثانية لمعرفة الإزاحة الزاوية التي قام بها خوان. باستخدام الصيغة الموصوفة أعلاه ، لديك θ = 35/7 = 5 راديان.

التمرين الثاني

إذا كان لديك ماريو الذي سافر في سيارته نصف مسار سباق دائري ، فما هو النزوح الزاوي الذي قام به ماريو؟?

حل

في هذا التمرين ، سيتم تطبيق الصيغة الأولى. نظرًا لأنه من المعروف أن ماريو سافر إلى نصف المسار ، فيمكن افتراض أنه بدأ السباق بزاوية 0 درجة وعندما وصل إلى منتصف الدائرة سافر 180 درجة. لذلك ، فإن الإجابة هي 180 درجة -0 ° = 180 ° = π راديان.

التمرين الثالث

ماريا بها بركة دائرية. يركض الكلب حول حوض السباحة على مسافة 18 مترًا. إذا كان نصف قطر المسبح 3 أمتار ، فما هو الإزاحة الزاوية التي صنعتها التميمة ماريا؟?

حل

نظرًا لأن المسبح دائري وتعرف نصف قطره ، يمكنك المتابعة لاستخدام الصيغة الثانية.

من المعروف أن نصف القطر يساوي 3 أمتار ، والمسافة التي قطعها الحيوان الأليف تساوي 18 مترًا. لذلك ، فإن الإزاحة الزاوية التي يتم تنفيذها تساوي 18 = 18/3 = 6 راديان.

مراجع

1. باستو ، جيه آر (2014). الرياضيات 3: الهندسة التحليلية الأساسية. مجموعة التحرير باتريا.
2. Billstein، R.، Libeskind، S.، & Lott، J. W. (2013). الرياضيات: نهج حل المشكلات لمعلمي التعليم الأساسي. لوبيز ماتيوس مونتيرز.
3. Bult، B.، & Hobbs، D. (2001). معجم الرياضيات (المصور إد). (F. P. Cadena، Trad.) Editions AKAL.
4. Callejo، I.، Aguilera، M.، Martinez، L.، & Aldea، C. (1986). الرياضيات. الهندسة. إصلاح الدورة العليا لـ E.G.B. وزارة التعليم.
5. Schneider، W.، & Sappert، D. (1990). دليل الرسم الفني العملي: مقدمة لأساسيات الرسم الفني الصناعي. Reverte.
6. توماس ج. ب. ووير ، م. د. (2006). الحساب: عدة متغيرات. بيرسون التعليم.